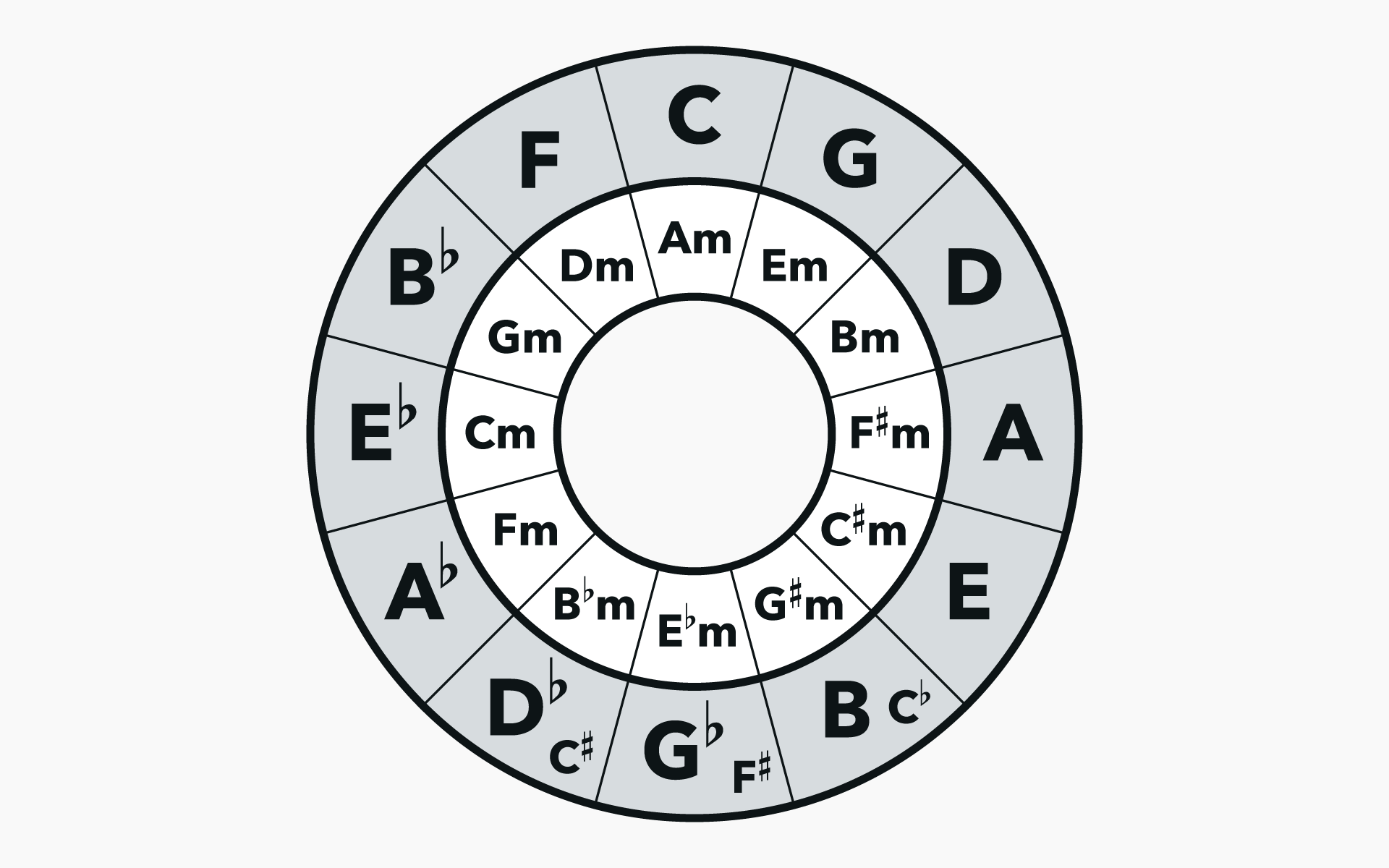
Circle of 5ths: The magic circle

Last time in my previous post, Majors and minors, I took the hard path and used the major diatonic formula to derive each major and minor chords and to make it easier to memorize/learn developed a personal approach to categorize the scales. Later, I’ve faced with a realization it all comes from a result of A minor diatonic scale already.

So, I can say, I am on the right way learning things, even tough it is the hard way but, this is life isn’t it? If you learn something in hard way, you’ll never forget.

If you’re into the algorithm in YouTube or IG, as you know, you can’t escape. And the algorithm was showing me a magic circle all the time, and one other thing which is the “CAGED system” which we’ll take a look later, I’ve decided to learn what that magic circle is and what it is used for.

Circle of fifths:

This circle is simply taking the fifth note of each note and connect them together. If you do that, you’ll see it will get back where it started and that’s why we call it a circle.

If we need to do that step by step, let’s start with C and write all triads Root 3rd 5th and connect them together until it reaches back to C again.

Remember the approach we applied last time,

• C F G no sharps and flats in major
• A D E taking sharps at 3rd note
• B is the problem child getting both sharped 3rd and 5th

C  E  G  => G  B  D  => D  F# A  => A  C# E  => E  G# B => B  D# F# 
                                                                 ||
  ===============================================================  
||
F# A# C# => C# F  G# => G# C  D# => D# G  A# => A# D  F => F  A  C

Now we know the fifth of each note, it is also possible to create a circle of relative minors by a simple trick:

• Either go 2 step back from the root (A =(-1)= B =(-1)= C)
• Or add 1 step to the 5fth (CEG =(+1)= A)

My understanding is if you really know triads well, memorize them so good, and use them for any kind of construction

• Finding relative minor (5th + 1)
  • C => CEG => G(+1) => Am
• Finding the 7th of the chord (Root - 1)
  • C => CEG => C(-1) => CEGA which is C7 chord
• Create a chord progression etc. etc. (I IV V => Root + (5th - 1) + 5th)
  • C => CEG => C + (G-1) + G => C F G

Anyway, these are some of my trick to find important info about the chords and scales. Now, lets build our circle of fifth by connecting them together and shape like a circle.

Before building the circle let’s also find all relative minors so we can display them in the circle.

C  E  G(Am)  => G  B  D(Em)  => D  F# A(Bm) => A  C# E(F#m) => E  G# B(C#m)=> B  D# F#(G#m)
                                                                                        ||
  ====================================================================================== 
||
F# A# C#(D#m)=> C# F  G#(Bbm)=> G# C  D#(Fm)=> D# G  A#(Cm) => A# D  F(Gm) => F  A  C(Am)

And finally add them on the circle to see the full picture.

                  ____C/B#___
    (C#/Dm) F/E# /    (Am)   \  G (Em)
                /             \
  (F#/Gm) Bb/A# |              |  D (Bm)
                |              |
  (B#/Cm) Eb/D# |              |  A (F#m)
                |              |
  (E#/Fm) Ab/G# |              |  E (C#m)
                \             /
  (A#/Bbm) Db/C# \___Gb/F#___/  B (G#m)
                   (Ebm/D#m)

Interesting key takeaways from

• if you go right you get 5th
• if you go left you get 4th
• there is a pattern repeating in majors and relative minors
  • F(at) C(ats) G(et) D(izzy) A(fter) E(ating) B(eads)
  • just bear in mind that there is no such thing as B# or E#

The reason why we get back to C is simple,

• We took 12 x 5th step, which is R(Whole)M2(Whole)M3(Half)P4(Whole)P5 in total 12 x 7 = 84 semitones/half
• In chromatic scale from C to C(octave)
  • C C# D D# E F F# G G# A A# B C (12 semitones/half = 1 octave)
• So if we take 84 steps, which is equivalent to 7 octaves.
  • The first C is 7 octaves lower than the last C in the circle.

Long story short, it is basically where 7(P5) and 12(Octave) first meets.

How to use circle of fifths

As a beginner musician, I can only derive this information by looking at the circle

• Create easily I-IV-V progression
  • C - F(left) - G(right)
    from previous post we know, 5th is the dominant so, C-F-G7-C
  • F# - C#(left) - B(right)
    same approach, 5th is the dominant so, F#-C#-B7-F#
• Create easily ii-V-I progression
  • ii is easy to find, R + M2(Whole), or look bottom left of the root on circle
    G(+1)=> A-G-D => Am-G7-D-Am
• And other chords progression as well..

What I use this circle mostly, is practicing. Find a cool chord you like its sound or a scale or triad or whatever use metronome and move around the circle.

As a summary, this circle gives us the information quickly if we know how to look at them. I am not at the level of jamming or composing/creating any music but I believe this one should be my second nature when I get that level to play smoothly and confidently.

Until next time,
Berk